Introduction

In this article i'm gonna present you a method to implement RegEx.

Link:

repo
Or on this website:
zip
Before the explanation, what even is RegEx ?
Regular Expressions are in fact a synthax allowing to find any pattern inside a text. A good RegEx dialect is Search Complete if it can, just by its synthax, find any pattern inside a text.
I'm not a huge fan of the actual synthax in the majority of the RegEx dialects. I was inspired by these dialects but tried to simplify them, in C++.
But first we have to define the characteristics of our dialect sensed to be Search Complete.

Allow set definition as a condition

This will be built by the introduction of a special character being - which will link the first to the last element of a set. For example, a-z will define to search for a character included between a et z according to the ASCII table.

Allow the repetition of a condition n times

This will be possible by the introduction of the following special characters { and } that will encompass a number designating the repetition of the previous condition.
For example a-z{5} will search for 5 contiguous characters between a and z.

Allow the repetition of a condition n times or more

This will be possible by the introduction of the special character '+' before the number declared between { et }
For example a-z{+5} will search for 5 or more contiguous characters between a and z.

Allow the not

It is already allowed if we put {0}

Allow the or context

This will be possible by the introduction of the following special characters [ and ]

We'll escape the special characters with \.

For example, [a-z{3}5-9{2}]{+2} will search for all the contiguous characters between a and z 3*2 = 6 times or more, or all the characters between 5 and '9 2*2=4 times or more.

- Ok, but what about the implementation?

Firstly it is important to note that the first condition is crucial.

Indeed, this condition tells us the possible patterns to match inside a text.

For example, if i have A-Za-z{8} as an regular Expression and

Pierre et Marie ont acheté une baguette à Joséphine ce midi.

We must first evaluate the entry points of the condition, here it's all the indices of the string that are an uppercase (since the first condition is A-Z/uppercase). The indices (starting from 0) are: [0, 10, 42].

So, the following algorithm will start from these indices to evaluate the remaining conditions of the regular Expression contiguously.

Testing the first index:

ierre is 5 characters long between a and z, it's to small because we want 8.

Next index, and it's the same, to small, 4 against 8 required.

Last index, we have 'oséphine' which is 8 characters long between a and z.

The Regular Expression will match for Joséphine.

Note that if we had A-Za-z{2}, the expression would match for Pierre because, even if ierre is 5 characters long, the expression will just search evaluate if the 2 next characters after P are between a and z.

To match with only 2 characters we must have this expression:

A-Za-z{2}a-z{0}

It means to match for an uppercase, then 2 lowercase, and then no lowercase.

An interesting and powerfull feature is to allow to a condition to match characters until a pattern. We will call it a break pattern.

This will be possible by the introduction of the character ? according to this way:

condition1{?condition2}

For example, A-Z[a-z{+1} {+1}]{?sympa} on Connais-tu un endroit sympa où l'on pourrait randonner ?

will match Connais-tu un endroit , all the lowercases, uppercases or space before the last pattern sympa.

Implementation details:

The programm requires 4 abstraction layers.

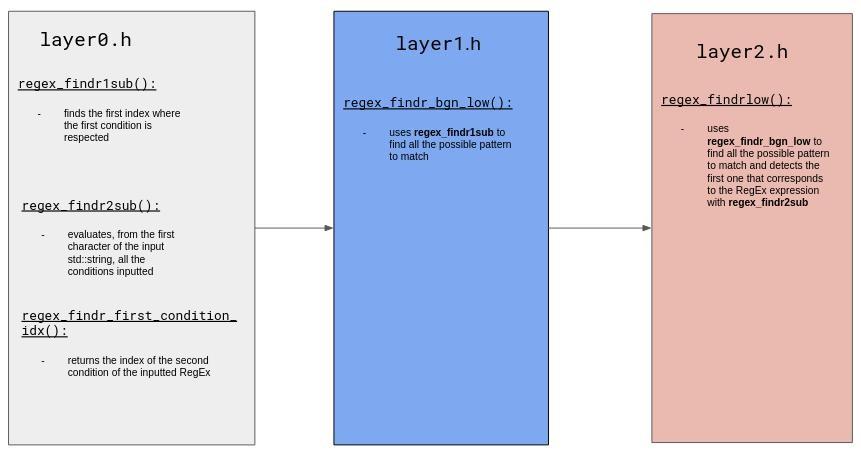
File 1:

A function is in charge to detect the first index in the character where a pattern to match could be located.
Another one evaluates the remaining conditions contiguously on the following characters.

File 2:

A function will use the 2 functions of the first file in order to filter the pattern to match.
At this point we already have a first version of our minimalist dialect taking in count all the mentioned features apart the break pattern.

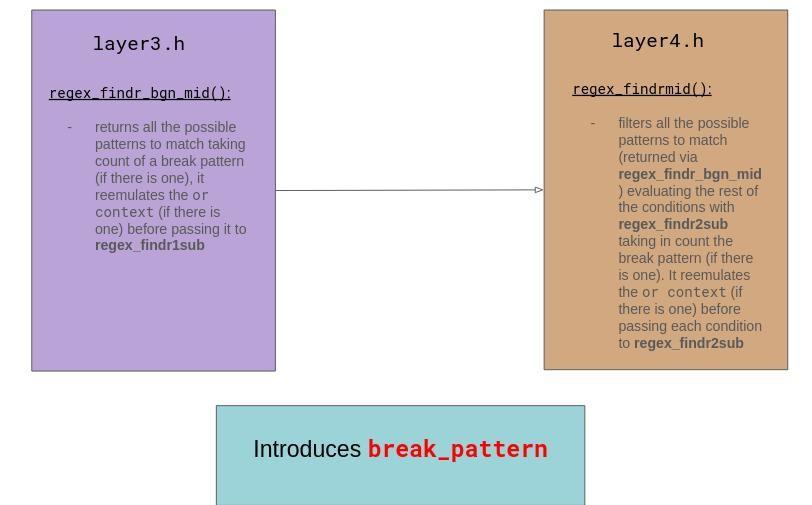
File 3:

A function is in charge to match matchable patterns. The latter will take in count the break pattern. To do so, the function will have to , before evaluating a condition, look if it has an associated break pattern and if yes, cut the text until the break pattern. After that the function will evaluate on the remaining cut text. If it is a success, then the remaining part of the text will be added to the cut part.

File 4:

The function will be in charge to filter the differents found matchable patterns by the previous function, contiguously evaluating the remaining conditions if there remains and taking in count the break pattern.

Conclusion:

The files 1 and 2 were used for the implementation of a first dialect that did not have the break pattern feature. Then the 2 other files took in count the break pattern feature because they were built on the first dialect.